Что такое инвестиционный риск и как его измерить?

В одной из своих прошлых статей я уже упрощенно касалась понятия доходности с поправкой на риск. Для того, чтобы адекватно ее анализировать, надо сначала определится с тем, что такое инвестиционный риск и главное, как его измерить.
Итак, наиболее общее определение: инвестиционный риск — это потенциальная возможность получить результат, не совпадающий с ожиданиями.
В англоязычной традиции довольно часто встречается понятие как отрицательного риска (downside risk), так и положительного (upside risk). То есть возможности того, что результат будет отличатся от ожиданий в лучшую, а не в худшую сторону. Лично меня от понятия положительного риска несколько коробит, однако многие метрики строятся таким образом, что действительно не отличают несчастных случаев от счастливых.
Приведенное выше определение риска сугубо качественное (но зато бесспорное) и не дает никаких идей касательно того, как его можно количественно измерить. Но для того, чтобы принимать обоснованные инвестиционные решения, нам нужна “метрика риска” (risk metric) — линейка, которой его можно измерить и выразить в численном виде.
Чтобы решить эту проблему, пойдем следующим путём: возьмем некоторый короткий горизонт инвестирования, скажем, 1 день. По прошествии одного дня мы можем посмотреть, какова была доходность инвестиции и записать результат в тетрадочку. Собственно, инвестировать для этого не обязательно, можно просто смотреть котировки на бирже. Еще через день у нас будет уже два результата, еще через день три и так далее. Если мы не оцениваем что-то уникальное (свежее IPO, например), то ждать тоже не надо — можно выгрузить массив исторических данных из архивов. Например, с finance.yahoo.com или morningstar.com.
Итак, каждый день наблюдений результат будет разный: в какие-то дни лучше, в какие-то хуже. В какие-то прибыль, в другие убыток. Собрав сравнительно большое количество таких ежедневных наблюдений, мы можем начать их обработку. Вычислим две характеристики:
- Среднее значение.
- Среднеквадратическое отклонение (СКО).
Первый параметр — это просто среднее арифметическое значение всех результатов, а вот по второму стоит пояснить подробнее.
Среднеквадратическое отклонение выборки (standard deviation) вычисляется по следующей формуле:
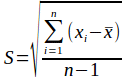
Где
S — среднеквадратическое отклонение,
n — количество наблюдений,
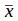 — среднее значение полученных наблюдений,
— среднее значение полученных наблюдений,
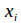 - наблюдение с номером i.
- наблюдение с номером i.
Не буду тут углубляться в вопрос, почему в знаменателе n-1, а не просто n, это длинная история, которая подробно разбирается в любом учебнике по теории вероятности.
Для того, чтобы пояснить на пальцах, зачем нужны эти два параметра, вспомним старую шутку про среднюю температуру по больнице. Итак, предположим у нас есть больница, в которой 10 пациентов (для простоты). Недавно директор нанял консультантов по управлению (скажем, McKinsey&Company или PWC), заплатил им денег, и те разработали новую бизнес стратегию. Согласно этой стратегии, зарплата главного врача должна быть привязана к ключевым показателям операционной эффективности. В ходе совместного обсуждения с консультантами было принято решение в качестве основного показателя применять среднюю температуру пациентов в больнице. Сказано — сделано. По результатам первого замера появляется таблица:
Средняя температура по больнице
| Пациент | Температура | Отклонение от среднего | Квадрат отклонения |
|---|---|---|---|
| 1 | 37,22 | 0,62 | 0,39 |
| 2 | 39,43 | 2,83 | 8,01 |
| 3 | 40,08 | 3,48 | 12,13 |
| 4 | 33,98 | -2,62 | 6,84 |
| 5 | 35,60 | -1,00 | 1,00 |
| 6 | 38,63 | 2,03 | 4,13 |
| 7 | 39,61 | 3,01 | 9,06 |
| 8 | 35,78 | -0,82 | 0,68 |
| 9 | 39,64 | 3,04 | 9,22 |
| 10 | 26,02 | -10,58 | 111,89 |
| Среднее: | 36,60 | СКО: | 4,26 |
К сожалению таблица не влезает на ваш экран. Попробуйте перевернуть телефон горизонтально или откройте страницу на десктопе.
Среднее по больнице ровно 36,6 — отличный результат, однако что-то тут не то. Особенно привлекает внимание пациент номер 10. Кажется, его уже можно выписывать.
Заподозрив неладное, собственник решил провести еще одно исследование: теперь замеры температуры проводятся у 10 сотрудников (то, что по правильному называется контрольная группа).
Средняя температура по контрольной группе
| Пациент | Температура | Отклонение | Квадрат отклонения |
|---|---|---|---|
| 1 | 36,62 | 0,02 | 0,0002 |
| 2 | 36,57 | -0,03 | 0,0007 |
| 3 | 36,62 | 0,02 | 0,0002 |
| 4 | 36,64 | 0,04 | 0,0013 |
| 5 | 36,61 | 0,01 | 0,0001 |
| 6 | 36,58 | -0,02 | 0,0004 |
| 7 | 36,64 | 0,04 | 0,0019 |
| 8 | 36,59 | -0,01 | 0,0001 |
| 9 | 36,57 | -0,03 | 0,0010 |
| 10 | 36,61 | 0,01 | 0,0001 |
| Среднее: | 36,60 | СКО: | 0,0259 |
К сожалению таблица не влезает на ваш экран. Попробуйте перевернуть телефон горизонтально или откройте страницу на десктопе.
Средняя температура по контрольной группе снова оказалась равна 36,6 однако есть одно очень важное отличие: СКО у сотрудников в 150 раз меньше, чем у пациентов. То есть во втором случае все полученные результаты распределены гораздо ближе к среднему, чем в первом.
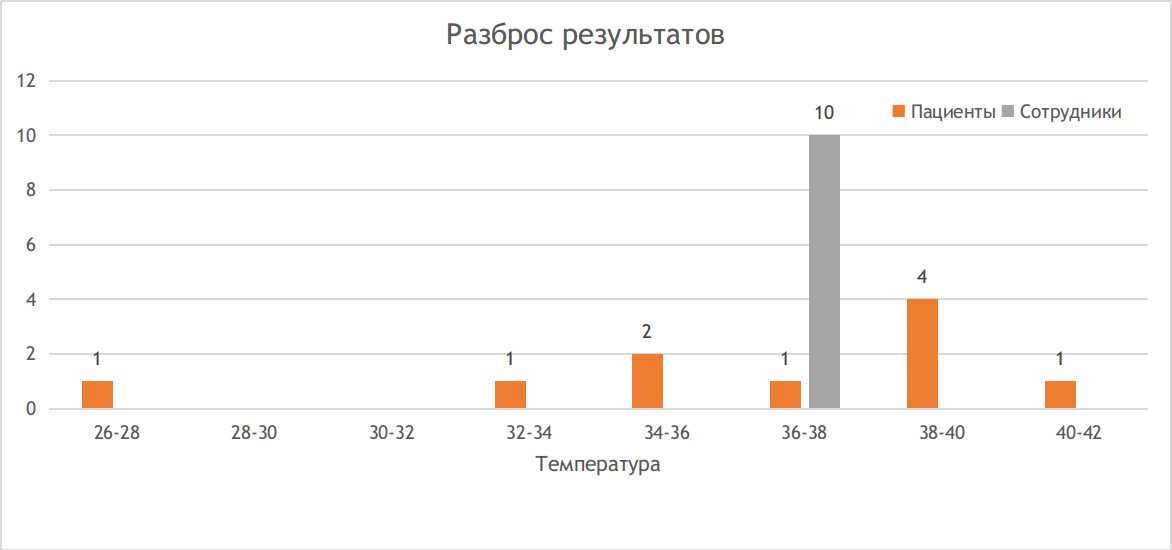
По этой причине можно говорить, что для людей в целом средняя нормальная температура равна 36,6, и это не смешно, а средняя температура по больнице уже шутка. Разница в разбросе значений.
Представление о риске как о СКО доходности
Идём дальше. Пусть наш высокооплачиваемый директор больницы решил инвестировать свои накопления во что-нибудь хорошее. Выбрал два инвестиционных фонда и вложил в каждый по 100 тыс. долларов.
Воодушевленный применением передового управленческого опыта на основной работе, он решил, что вознаграждение управляющих активами будет тоже жестко привязано к результату. В данном случае — к полученной доходности. По прошествии 10 недель наш воображаемый инвестор решил посмотреть на результаты и проанализировать, что получается.
Результат по фонду А
| Неделя | Баланс (тыс USD) | Прибыль/убыток | Отклонение от среднего | Квадрат отклонения |
|---|---|---|---|---|
| 0 | 100 |
|
|
|
| 1 | 101,01 | 1,01% | 0,39% | 0,0015% |
| 2 | 100,50 | -0,50% | -1,12% | 0,0125% |
| 3 | 97,60 | -2,89% | -3,51% | 0,1230% |
| 4 | 102,66 | 5,18% | 4,57% | 0,2084% |
| 5 | 102,77 | 0,10% | -0,52% | 0,0027% |
| 6 | 104,75 | 1,93% | 1,31% | 0,0171% |
| 7 | 105,42 | 0,64% | 0,03% | 0,0000% |
| 8 | 105,84 | 0,39% | -0,23% | 0,0005% |
| 9 | 107,20 | 1,29% | 0,67% | 0,0045% |
| 10 | 106,16 | -0,97% | -1,59% | 0,0253% |
|
|
Среднее: | 0,62% | СКО: | 2,10% |
Результат по фонду Б
| Неделя | Баланс (тыс USD) | Прибыль/убыток | Отклонение от среднего | Квадрат отклонения |
|---|---|---|---|---|
| 0 | 100 |
|
|
|
| 1 | 101,92 | 1,92% | 0,76% | 0,0058% |
| 2 | 100,81 | -1,09% | -1,71% | 0,0291% |
| 3 | 94,91 | -5,85% | -6,47% | 0,4187% |
| 4 | 104,92 | 10,54% | 9,92% | 0,9845% |
| 5 | 105,02 | 0,10% | -0,52% | 0,0027% |
| 6 | 108,87 | 3,67% | 3,05% | 0,0929% |
| 7 | 110,12 | 1,14% | 0,53% | 0,0028% |
| 8 | 110,84 | 0,66% | 0,04% | 0,0000% |
| 9 | 113,46 | 2,36% | 1,74% | 0,0304% |
| 10 | 111,29 | -1,92% | -2,53% | 0,0642% |
|
|
Среднее: | 1,15% | СКО: | 4,26% |
Если посмотреть на полученную доходность, то видно, что однозначный лидер — это фонд Б. За рассматриваемые 10 недель получена накопленная доходность в 11,29% против 6,16% у фонда А, почти в 2 раза больше.
Казалось бы, вопрос решен, надо забирать все деньги из фонда А и перекладывать в фонд Б, однако не всё так просто. Как вы уже наверняка заметили, несмотря на то, что средняя доходность, показанная фондом Б, значительно выше, чем у фонда А, разброс результатов тоже гораздо больше. Численно это видно в том, что СКО результатов фонда Б тоже выше, чем у фонда А, причем чуть больше чем в 2 раза.
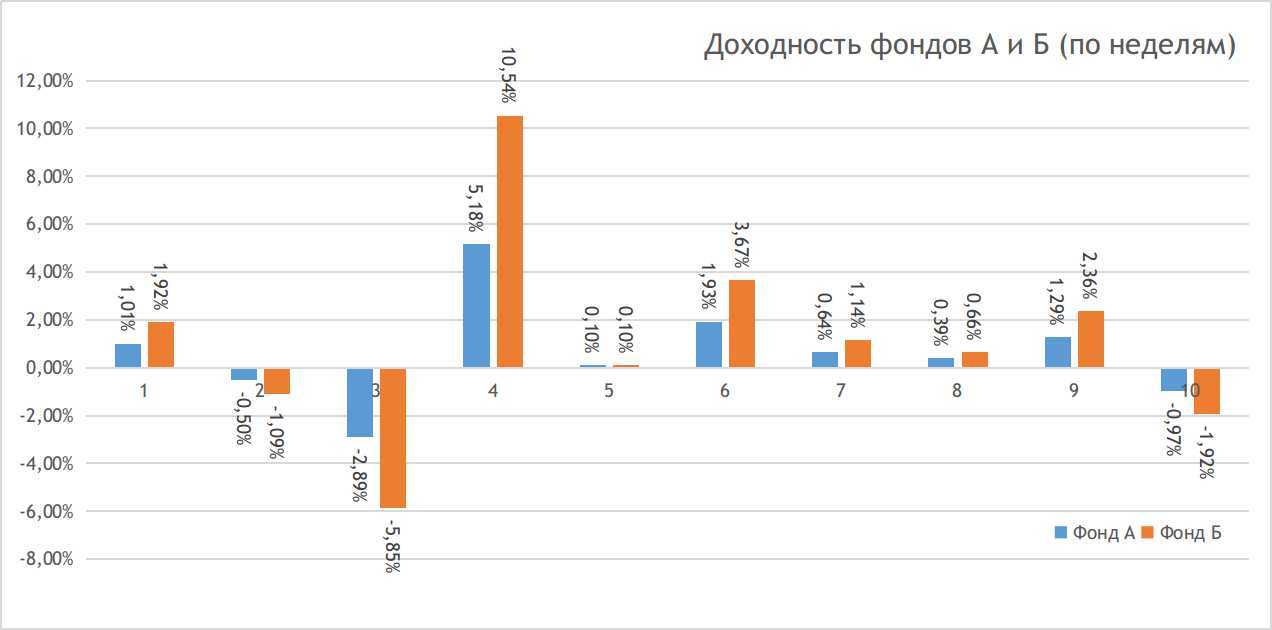
Раскрою карты — оба фонда в этом примере инвестируют в один и тот же актив: индекс S&P500. Я взяла исторические данные по реальным котировкам этого индекса за 10 недель где-то в середине 19 года и использовала их в таблице.
Единственная разница в том, что фонд Б инвестирует с двойным плечом. То есть на каждый доллар, вложенный инвесторами, привлекает еще один доллар заемных средств. Если бы кредит был под нулевую ставку, то результат фонда Б был бы четко равен результату фонда А, умноженному на 2. Однако поскольку за пользование деньгами надо платить (в моём примере порядка 5% годовых), доходность становится несколько ниже, а колебания немного шире.
Еще раз: в итоге получается, что инвестор получает увеличенный доход, но только за счет увеличения риска. То есть благодаря использованию кредита его ожидаемые прибыли увеличиваются, но ровно также увеличиваются и вероятные убытки.
Понять это мы можем, посмотрев на показатель СКО, который показывает разброс полученных результатов. Думаю, после всего сказанного выше никого не удивит предложение использовать этот критерий как измеритель инвестиционного риска.
Действительно, этот подход нашел очень широкое применение, начиная как минимум с работ Марковица 50-х годов. А может и раньше. В очень большом количестве учебников, по сути, предполагается:
риск == среднеквадратическое отклонение доходности
И это утверждение воспринимается как аксиома. Именно на этом строятся наиболее распространенные метрики доходности с поправкой на риск, но это тема для отдельной статьи.
Очень часто можно встретить графическое изображение активов на плоскости с двумя координатами: по одной оси средняя доходность, а по другой оси ее СКО.
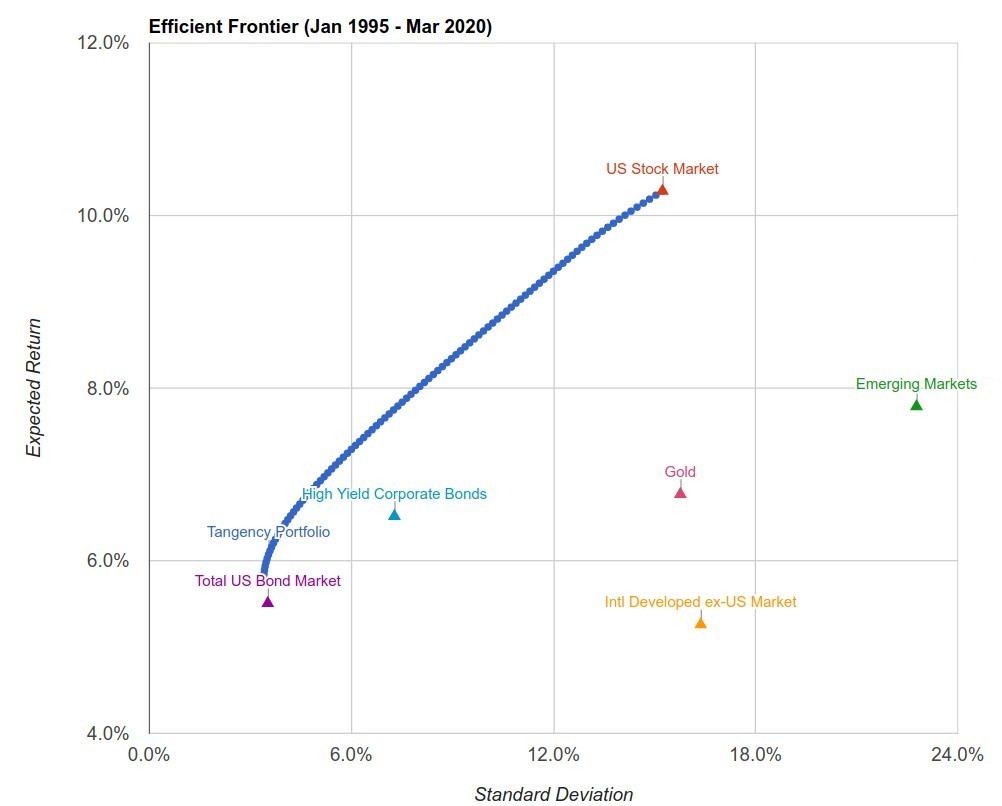
Генератор отчетов Interactive Brokers позволяет автоматически вычислять СКО для портфеля и заданных бенчмарков (раздел Risk Measures Benchmark Comparison).
Однако несмотря на то, что СКО является важнейшим показателем риска портфеля, у него есть ряд недостатков. Как, впрочем, и у всех остальных, но это тоже тема для отдельной статьи.





 soxic6
soxic6
