Что такое оптимизация инвестиционного портфеля

В этой статье я постараюсь изложить теорию, известную в России как современная теория портфеля (modern portfolio theory − MPT). В англоязычной литературе чаще встречается термин mean-variance optimization (MVO), но я затрудняюсь найти ему адекватное русское соответствие. Я постараюсь изложить основные принципы, рассказать о ее достоинствах и, конечно же, о недостатках, которых имеется в изобилии.

Традиционно основателем теории считается Гарри Марковиц, сформулировавший ее основные принципы в 1952 году (так что теорию довольно сложно назвать “современной”). Далее в 1964 году идеи Марковица существенно расширил Уильям Шарп, который, помимо прочего, ввел в употребление модель CAPM, идеологически тесно связанную с современной теорией портфеля.

Я предлагаю рассматривать модели, созданные этими авторами, как своеобразный “ветхий завет” портфельных инвестиций. На современном этапе построенная ими картина мира кажется чрезмерно упрощенной. Хотя существуют приверженцы ортодоксального взгляда, настаивающие, что идеи отцов-основателей надо понимать буквально.

Многие более поздние исследователи существенно расширили базовую модель, предложив различные варианты по преодолению наложенных на нее ограничений. Например, Трейнор и Блек в 1973 году, Гринолд в 1989, Блек и Литтерман в 1992. Однако эти методы и модели лежат за пределами данной статьи, темой которой является именно ортодоксальный подход. Полное описание всех возможных вариантов займет как минимум книгу (а скорее всего − не одну).

Базовые идеи современной теории портфеля

Итак, рассматривается задача со следующими исходными данными:

1. Имеется гипотетический инвестор с фиксированным и известным горизонтом инвестирования \(T_H\).
2. В его распоряжении имеется большое (желательно бесконечно большое) количество различных активов, в которые можно инвестировать.
3. Активы можно комбинировать, получая таким образом инвестиционный портфель. В классической постановке допускаются только положительные веса, однако теорию не сложно обобщить также на случай, когда разрешены и отрицательные веса (то есть короткие позиции).

Вопрос формулируется так: как распределить капитал между активами оптимальным образом?

Вопрос выбора критерия оптимальности я рассмотрю более подробно ниже. Пока хочу обратить внимание на первое существенное ограничение: считается, что инвестор имеет фиксированный и известный горизонт инвестирования.

Однако на практике инвестор, как правило, определяет срок инвестирования лишь примерно. Скажем, планирует накопить на пенсию, которая наступит через неопределенный промежуток времени, но не раньше чем через 10 лет. Более того, нет никаких гарантий, что он не пересмотрит свое видение через несколько лет и не поменяет свои планы, как в сторону сокращения, так и в сторону увеличения срока.

Очевидно, что при жестко заданном сроке инвестирования для каждого актива можно построить какой-то прогноз по его доходности. Для некоторых активов эта доходность будет гарантированной, такие активы будем называть безрисковыми (risk free assets). Традиционно считается, что безрисковые активы − это краткосрочные обязательства казначейства США или застрахованные депозиты в надежных банках. Но можно также принять, что безрисковых активов не существует. Для модели оптимизации это не принципиально.

Для других активов точный прогноз сделать нельзя, но можно оценить вероятность того или иного исхода. Это рисковые активы (risky assets).

То есть еще раз: предполагается, что для рисковых активов можно так или иначе определить математическое ожидание доходности (за время инвестирования \(T_H\) ) и ее статистические характеристики: момент второго порядка − дисперсию (variance) и высших порядков, если нужно.

Обращаю внимание, что мы не налагаем каких-то ограничений на форму распределения вероятности − оно может быть какое угодно, и каждый актив может иметь свое распределение. Нужно, чтобы у каждого актива оно в принципе было.

Фундаментальная проблема: применимость вероятностей вообще.

Что мы имеем в виду, когда говорим о той или иной вероятности получения доходности?

На самом деле, это вопрос сложный. Гораздо сложнее, чем кажется на первый взгляд. Как известно, в математике понятие вероятности вводится для событий, которые, хотя бы теоретически, могут быть повторены любое число раз при одних и тех же условиях.

Классический пример − это бросание монеты, которое можно повторять столько раз, сколько нужно. В этом случае, вероятность выпадения орла в 50% означает, что чем больше делается повторов, тем больше приближается среднее количество орлов к 50%. Чем короче серия подбрасываний (меньше выборка), тем дальше может быть среднее выборочное значение от теоретически идеальной величины 50х50. Про результат единичного бросания вообще ничего нельзя сказать, кроме того, что выпадет либо орел, либо решка.

А что означает, скажем, вероятность 50% получить прибыль в 10% на инвестиционном горизонте 10 лет?

Для того, чтобы это понять, надо вообразить инвестора, который имеет возможность вернуться назад в прошлое и прожить этот период заново. Я понимаю, что это звучит странно, но так оно и есть. Для того, чтобы получить множество повторных реализаций, нужно иметь возможность прожить один и тот же период много раз. Тогда по мере увеличения числа попыток (размера выборки) среднее количество реализаций, в которых инвестор получил доходность в 10%, будет стремится к 50%.

Может быть, проще представить второй вариант интерпретации: множество параллельным миров (бесконечно большое множество), в каждом из которых реализовалась своя версия истории. Тогда в половине этих миров инвестор получил доходность 10%, а в другой половине реализовались какие-то другие сценарии.

Можно возразить, что если горизонт инвестирования, скажем, 1 год, то тогда ближайший год − это первая реализация, следующий год − это вторая, потом третья и так далее. Имея суммарный горизонт инвестирования, скажем, 30 лет, набранный из меньших интервалов по одному году, мы и получим требуемую выборку.

Более того, к выборке из 30 реализаций уже можно попробовать применить центральную предельную теорему (закон больших чисел) и утверждать, что результат инвестирования будет распределен нормально, независимо от того, какую форму имеют распределения в каждый конкретный год.

Однако это рассуждение не верно. Для того, чтобы смело усреднять, надо, чтобы все повторы происходили в абсолютно идентичных условиях. Но мир через год будет уже не такой, как сейчас. Через два года он будет отличаться еще больше, а через 29 лет, может быть, вообще не будет иметь с миром сегодняшним ничего или почти ничего общего.

Это означает, что усредняя доходность и дисперсию за 30 лет, мы по факту получаем не среднее от 30 реализаций одной случайной величины, а средние от 30 разных случайных величин по одной реализации. Это будет одно и то же только в случае, если случайный процесс обладает свойством эргодичности. Но в применении к доходности финансовых инструментов это крайне маловероятно.

Процесс оптимизации инвестиционного портфеля

Тем не менее отвлечемся от фундаментальных проблем и вернемся к процессу оптимизации.

Рассмотрим для начала частный случай 2 доступных активов. Как уже говорилось выше, предположим, что каким-то образом для каждого из них сформирован прогноз, включающий:

• математическое ожидание доходности,
• дисперсию доходности,
• корреляцию активов друг с другом.

Тогда можно записать соотношения:

$$ r_p = w_1 r_1 + w_2 r_2 \; \; \; (1) $$ $$ \sigma_p^2 = w_1^2 \sigma_1^2 + w_2^2 \sigma_2^2 + 2 w_1 w_2 \rho \sigma_1 \sigma_2 \; \; \; (2)$$

Где:

\( r_p \) − ожидаемая доходность портфеля;

\( w_1 \) − вес в портфеле актива 1;

\( r_1 \) − ожидаемая доходность актива 1;

\( w_2 \) − вес в портфеле актива 2;

\( r_2 \) − ожидаемая доходность актива 2;

\( \sigma_p^2 \) − дисперсия доходности портфеля;

\( \sigma_1^2 \) − дисперсия доходности актива 1;

\( \sigma_2^2 \) − дисперсия доходности актива 2;

\( \rho \) − коэффициент корреляции активов 1 и 2.

Для портфеля из двух активов можно также записать:

$$ w_1 + w_2 = 1 $$

Как уже писалось выше, веса обычно предполагаются не отрицательными, то есть короткие позиции запрещены. Однако все соотношения остаются верны и в случае, когда отрицательные веса тоже разрешены.

Для примера возьмем следующие активы:

• Актив 1: ожидаемая доходность \(r_1=6%\); СКО \( \sigma_2=4% \)
• Актив 2: ожидаемая доходность \(r_2=10%\); СКО \( \sigma_2=16% \)

Что примерно соответствует историческим показателям рынка облигаций США (актив 1) и индекса S&P500 (актив 2) за период с 1987 по 2020 год.

Представим наши активы графически в виде точек на плоскости. По горизонтальной оси будем откладывать ожидаемое среднеквадратическое отклонение (корень из дисперсии), а по вертикальной оси математическое ожидание доходности.

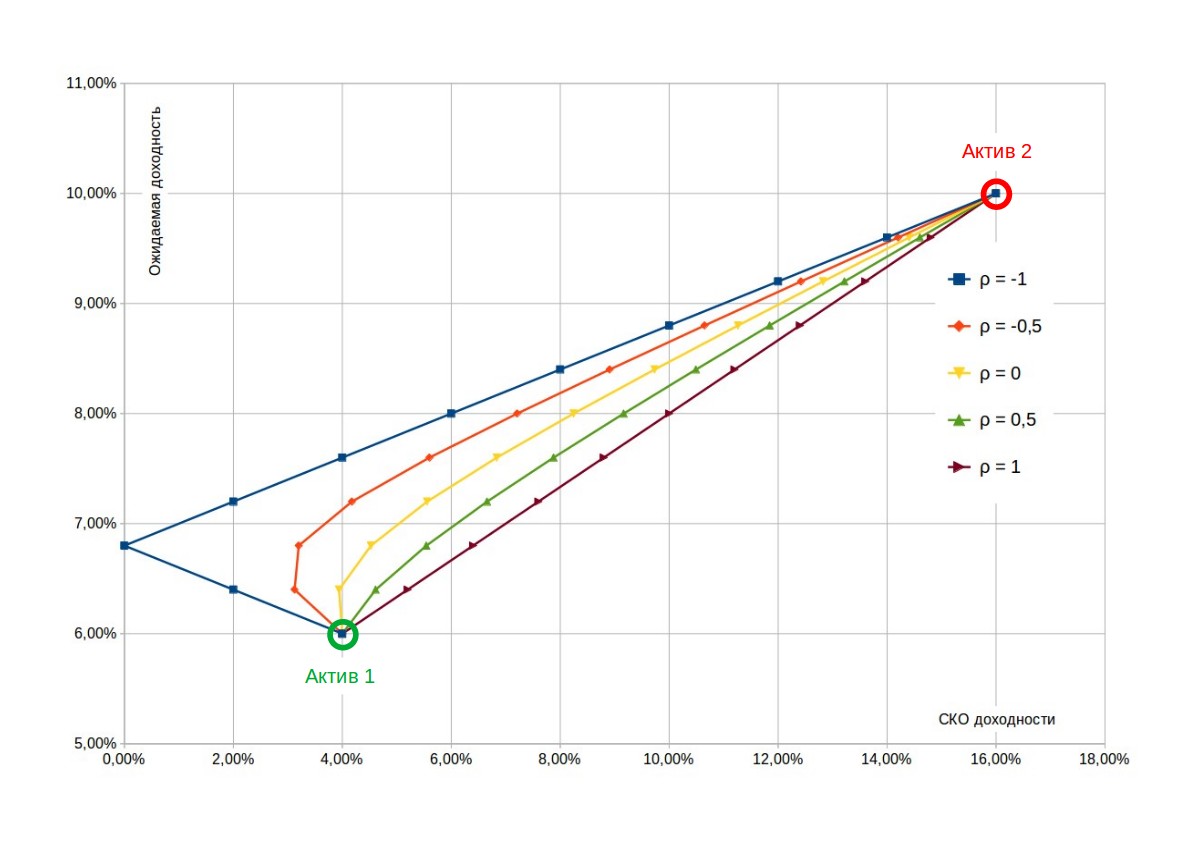
Теперь можно нанести на график все возможные варианты портфелей.

На графике множество возможных комбинаций представляет собой линию, форма которой зависит от коэффициента корреляции между активами. На рисунке показано несколько характерных случаев:

• При коэффициенте корреляции \( \rho = 1 \) множество возможных портфелей представляет собой прямую линию, проходящую через оба актива. Диверсификация не дает преимуществ, так как доходность активов падает и растет синхронно.
• При коэффициенте корреляции \( \rho = -1 \) множество портфелей превращается в своеобразный повернутый шеврон с вершиной на вертикальной оси. То, что вершина находится на оси, означает, что СКО такого портфеля \( \sigma_p = 0 \).

Таким образом, имея пару активов с идеальной антикорреляцией и при этом положительной ожидаемой доходностью, их можно было бы скомбинировать в портфель в таких соотношениях, что доходность портфеля будет гарантированной. То есть инвестиция станет безрисковой. К сожалению, идеальная антикорреляция на практике не встречается.

Требования положительной доходности обоих активов исключает возможность открытия одновременно длинных и коротких позиций по какому-то инструменту, поскольку их доходности имеют противоположные значения, а значит не могут быть положительны одновременно.

Следуя традиции современной теории портфеля, я буду далее считать, что:

Инвестиционный риск == среднеквадратическое отклонение доходности

Хотя такое предположение вовсе не является само собой разумеющимся и имеет ряд недостатков.

Принимая такой подход, мы косвенно считаем, что абсолютно вся информация об инструменте содержится в его цене. То есть если цена на инструмент стабильна, то и риск низок. Это видение довольно спорно. Например облигация спекулятивного класса может иметь очень стабильную цену, однако при этом очень высокий риск, связанный с дефолтом эмитента. Есть ряд вариантов модификации теории для учета “скрытых рисков”, однако мы не будем тут их касаться.

Вернемся к графику. При значениях коэффициента корреляции, находящихся в промежутке между крайними значениями, множество возможных портфелей будет представлять из себя горизонтальную параболическую кривую, проходящую через актив 1 и актив 2. Можно заметить, что в некоторых случаях вершина этой параболы находится левее и выше, чем актив 1.

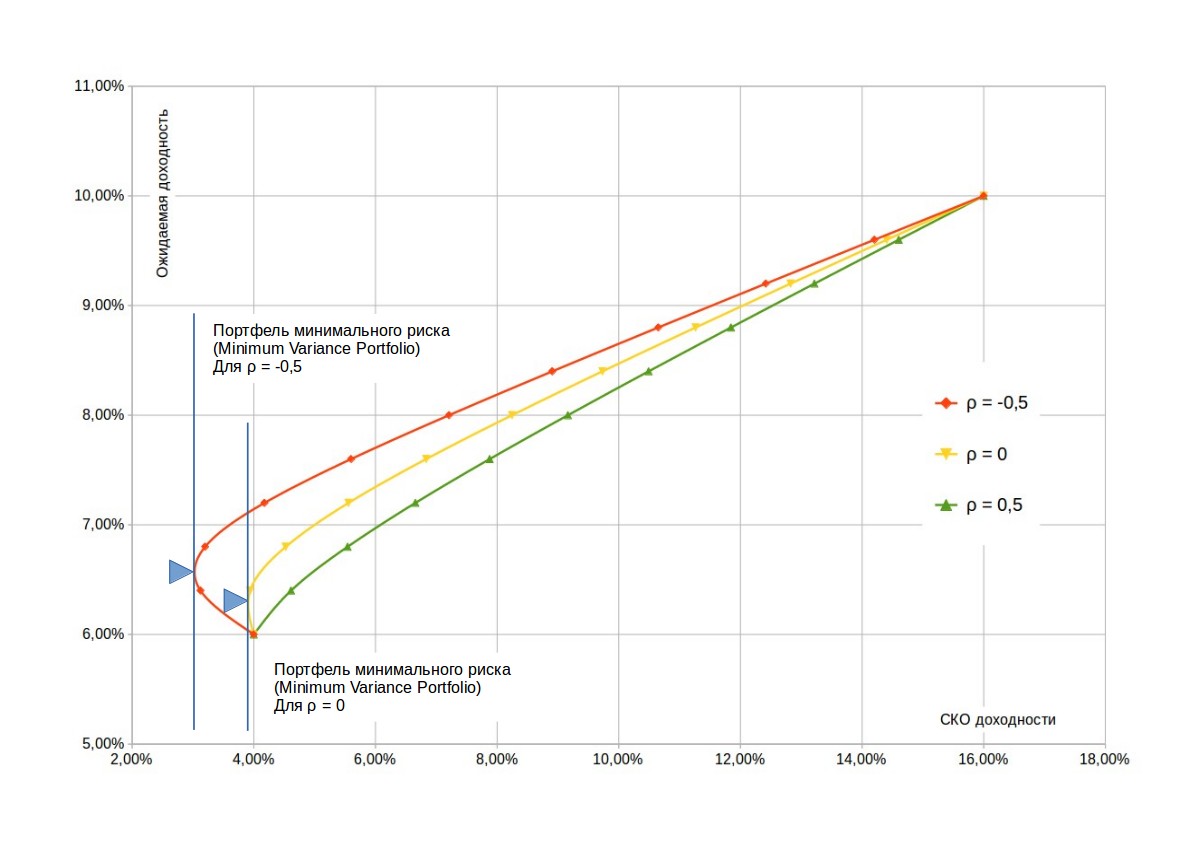
Это означает, что существует возможность собрать портфель с риском ниже, чем риск самого консервативного актива в портфеле, и при этом с более высокой доходностью. Это и есть преимущество от диверсификации активов. Данное заключение является одним из наиболее важных выводов теории.

Такая возможность есть не всегда, а только в том случае, если активы обладают низкой или лучше отрицательной корреляцией. Так, например, для случая \(\rho = 0,5\) вершина параболы расположена таким образом, что минимальный риск достигается в частном случае портфеля, состоящего на 100% из актива 1.

Отмечу, что ожидаемая доходность портфеля в этой модели не может быть выше, чем доходность самого доходного актива.

Обойти это ограничение возможно, но только в случае, если мы предполагаем, что инвестор совершает с портфелем некоторые манипуляции, тем или иным образом. Например, по самому простому алгоритму: просто восстанавливает исходные доли активов в портфеле (такая процедура часто называется ребалансировкой).

Однако тогда модель превращается в многопериодную, то есть предполагается, что есть множество периодов инвестирования, и в конце каждого периода инвестор принимает определенные решения.

Есть и более сложные варианты, чем ребалансировка. Например, в методике адаптивного распределения активов (adaptive asset allocation) инвестор в конце каждого периода заново выполняет оптимизацию портфеля, включая в модель новые данные. Но рассмотрение этой методики заслуживает отдельной статьи.

Обобщение на множество активов

Теорию легко обобщить на случай любого конечного числа активов. Характеристики риска и доходности портфеля будут тогда определяться соотношениями:

$$ r_p = w_1 r_1 + w_2 r_2 + ... w_i r_i = \sum_{i=1}^n {w_i r_i} \; \; \; (3) $$ $$ \sigma_p^2 = \sum_{i=1}^n { \sum_{j=1}^n { w_i w_j \rho_{ij} \sigma_i \sigma_j } } \; \; \; (4)$$ $$ \sum_{j=1}^n { w_i } = 1 $$

Где:

\( r_p \) − ожидаемая доходность портфеля;

\( w_i \) − вес в портфеле i-го актива;

\( r_i \) − ожидаемая доходность i-го актива;

\( \sigma_p^2 \) − дисперсия доходности портфеля;

\( \sigma_i^2 \) − дисперсия доходности i-го актива;

\( \rho_{ij} \) − коэффициент корреляции активов i и j.

Добавим к нашему предыдущему примеру еще один актив со следующими характеристиками:

• Актив 3: ожидаемая доходность \(r_1=9,5%\); СКО \( \sigma_2=19,6% \),

что примерно соответствует индексу акций компаний малой капитализации США (в период с 1987 по 2020 годы).

Предположим следующую корреляционную матрицу:

$$ \rho = \begin{bmatrix} 1 & 0,1 & 0\\ 0,1 & 1 & 0,85\\ 0 & 0,85 & 1\end{bmatrix} $$

Которая также примерно соответствует историческим данным по выбранным нами активами за период с 1987 по 2020 год.

Отобразим все возможные портфели графически в координатах риск − ожидаемая доходность.

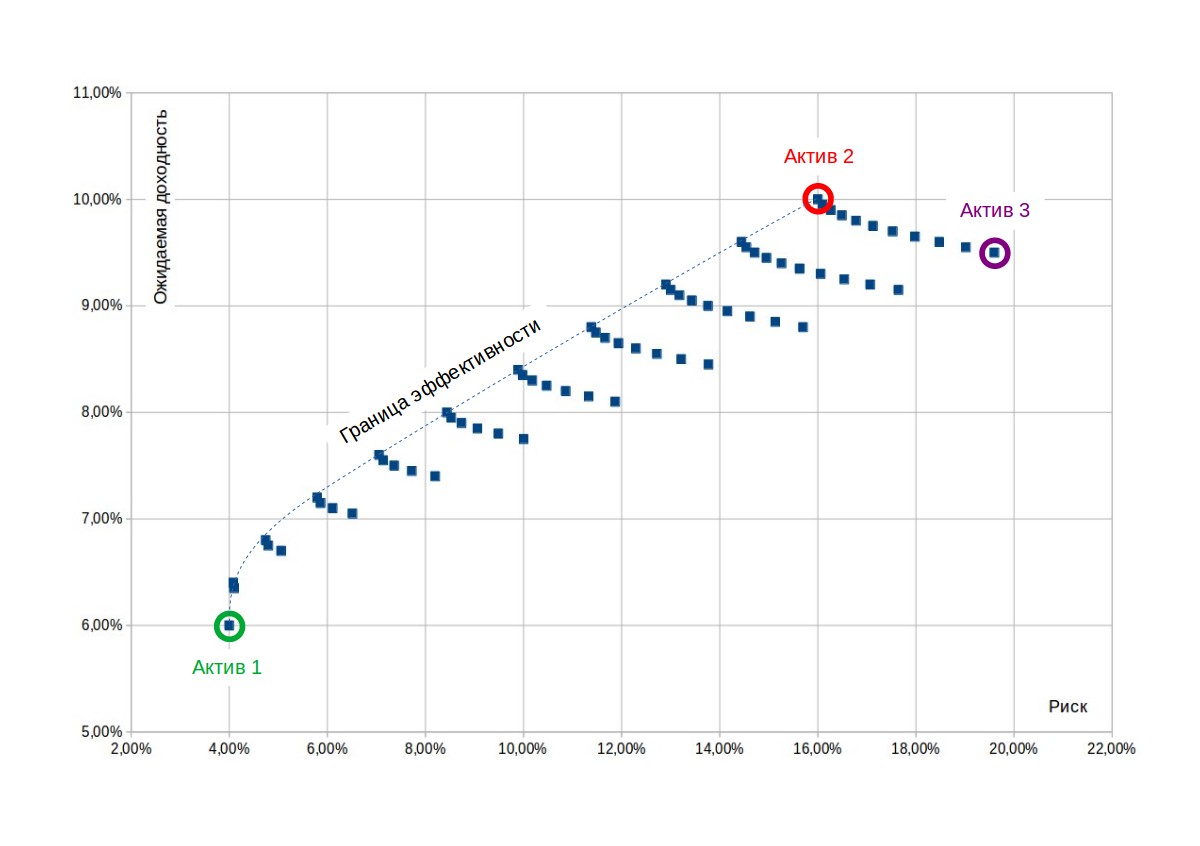
Теперь множество возможных портфелей представляет собой не линию, а область.

Точки на графике представляют собой различные варианты комбинации активов с шагом весов в 10%, но возможны любые промежуточные значения.

Зададимся каким-либо значением ожидаемой доходности (например, 9%). Данную доходность можно получить при помощи бесконечного количества сочетаний активов, однако одно из сочетаний будет отличаться от остальных тем, что обеспечит при данной доходности минимальный уровень риска. Такой портфель будет соответствовать точке на левой верхней границе области.

Эта граница называется границей эффективности портфеля. Каждая точка на ней соответствует портфелю, который позволяет обеспечить минимально возможный риск при данной доходность или, что то же самое, максимальную доходность при заданном уровне риска.

Граница эффективности, построенная в данном примере, имеет интересную особенность. На самом деле она полностью совпадает с границей эффективности для 2 активов: актива 1 и актива 2. То есть добавление третьего актива не приносит дополнительных преимуществ, а граница эффективности остается там же, где и была.

Таким образом дополнительная диверсификация имеет смысл, только если новый актив имеет положительную доходность и при этом достаточно низкую, а лучше отрицательную корреляцию с другими активами портфеля. Этот вопрос будет подробнее рассмотрен в следующем разделе.

Критерий Шарпа

Теоретически, с позиций описанной выше модели, рациональному инвестору нет смысла инвестировать в портфели за пределами границы эффективности, так как они либо при той же доходности имеют более высокий риск, либо при том же риске имеют более высокую доходность.

Конечно, к выбору портфелей можно добавить какие-либо дополнительные соображения. То есть ввести некоторый критерий качества, который будет учитывать что-то еще. Например, добавить требование, чтобы портфель состоял не менее чем из трех активов или чтобы доля каждого актива не превышала, скажем, 25%, или какие-либо другие. Но тогда это будет уже другая модель.

Но вернемся к ортодоксальной теории. Предположим, что есть некоторая доходность \( r_f \) которую можно получить, не принимая на себя никаких рисков. То есть такую, что \( \sigma_f=0 \). Тогда для каждого портфеля можно ввести показатель:

　　$$ S_p = {{r_p - r_f } \over \sigma_p} $$

Где:

\( S_p \) − коэффициент Шарпа для данного портфеля;

\( r_p \) − ожидаемая доходность портфеля;

\( r_f \) − безрисковая доходность;

\( \sigma_p \) − риск портфеля.

Значение коэффициента Шарпа показывает, сколько доходности получает инвестор на каждую единицу принятого на себя риска. Данный критерий нашел широчайшее применение в портфельной теории и является классической метрикой доходности с поправкой на риск.

Портфели с большим коэффициентом Шарпа можно считать более эффективными, так как они позволяют получить доходность по меньшей “цене”.

Введение критерия Шарпа позволяет сократить границу эффективности до одного портфеля – портфеля, который позволяет получить максимальный коэффициент Шарпа.

Посмотрим, как это выглядит графически. Для примера снова возьмем те же активы 1 и 2 и предположим между ними небольшую положительную корреляцию с \( \rho=0,1 \). Это примерно соответствует корреляции между доходностями индекса S&P 500 и индекса облигаций США с 1987 по 2020 годы.

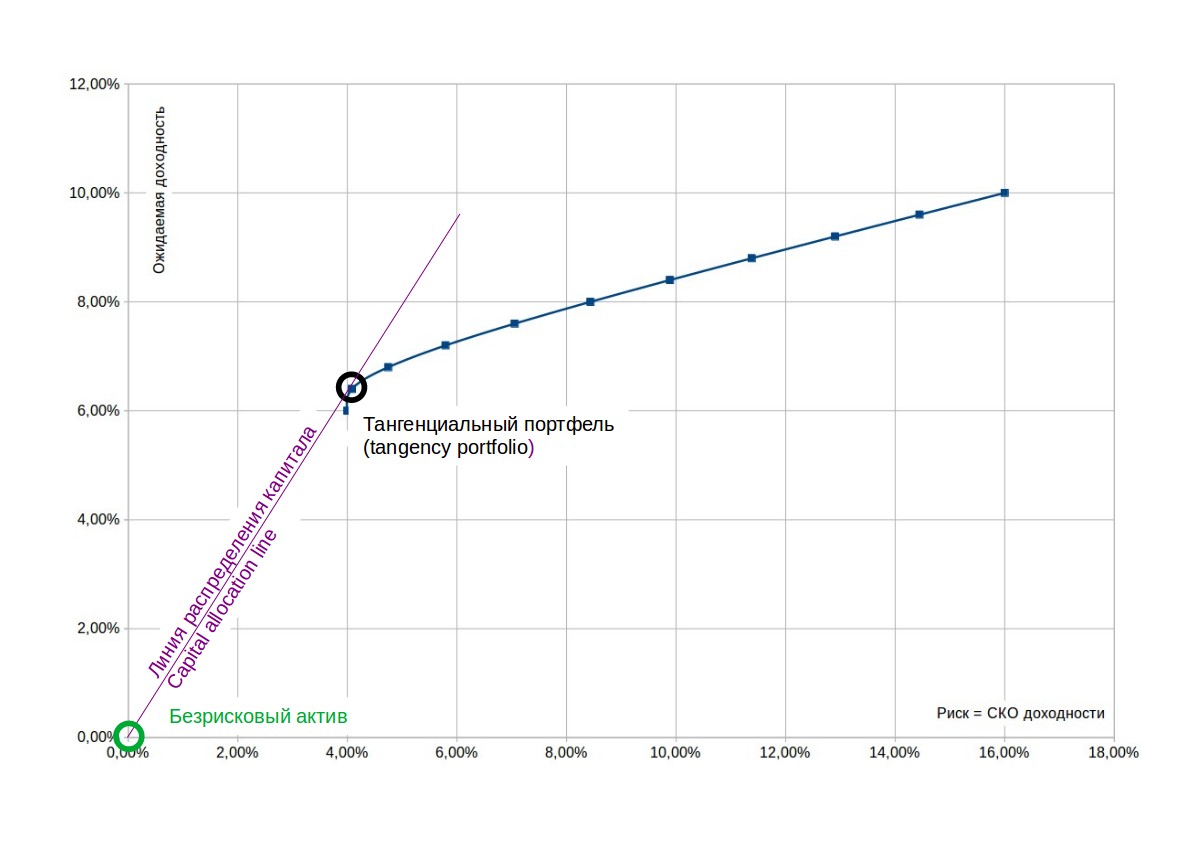
На момент написания этой статьи (июнь 2020 года) получить безрисковую доходность практически невозможно, поэтому положим \( r_f=0 \). В такой постановке безрисковый актив будет совпадать с началом координат, однако все рассуждения возможны для произвольного положения безрискового актива на вертикальной оси.

Коэффициент Шарпа для любого портфеля (или отдельного актива) будет представлять собой тангенс угла наклона линии, проходящей через точку, отображающую портфель, и через безрисковый актив.

Соответственно, для того чтобы найти оптимальный по Шарпу портфель, нужно построить из безрискового актива касательную к границе эффективности. Точка пересечения будет представлять собой оптимальный портфель по соотношению доходности и риска. По понятным причинам такой портфель иногда называют касательным (tangency portfolio). В нашем примере такой портфель примерно на 15% состоит из индекса S&P 500 и на 85% из облигаций.

На графике видно, что оптимальный по Шарпу портфель очень близок к портфелю с минимальным риском (minimum variance portfolio), и на практике это типичная ситуация, однако с теоретической точки зрения это два разных портфеля, которые вовсе не обязаны совпадать или быть как-то близки друг к другу.

Проблемы теории

Выше я изложила базовые идеи современной теории портфеля, и сейчас хочу подробнее поговорить о ее проблемах. Большая часть этих сложностей известна давно, и предложен ряд вариантов их преодоления, но полное перечислений возможных модификаций выходит далеко за рамки данной статьи.

Главная проблема, вероятно, уже стала очевидной читателю: это неопределенность исходных данных.

Еще раз повторю, исходными данными для модели являются ожидаемые доходности и риски финансовых инструментов на заданном инвестиционном горизонте. Но откуда их взять?

Один из возможных ответов − оценить по историческим данным. В примерах выше мы поступали просто:

1. Брали исторические данные о доходности инструментов с 1987 по 2020 год.
2. По этим данным оценивали значения доходности и риска.
3. Использовали эти оценки как входные данные модели.

Но такой подход требует принятия очень серьезного допущения. Нужно иметь уверенность, что будущее будет точно таким же, как прошлое.

Если посмотреть на проблему глубже, то можно увидеть, что даже такой упрощенный подход приводит к сложностям. Проблема в том, что оценки параметров существенно зависят от выбора исторического периода, по которому проводится оценка (lookback period). Этот период я в дальнейшем буду называть статистической базой.

Параметры модели в зависимости от статистической базы

	Параметр	1987-2020	1997-2020	2007-2020
Индекс облигаций США (актив 1)	\( r \)	5,96%	5,07%	4,41%
	\( \sigma \)	3,81%	3,43%	3,34%
Индекс S&P 500 (актив 2)	\( r \)	10,16%	8,14%	7,99%
	\( \sigma \)	15,08%	15,36%	15,41%
Индекс малых компаний (актив 3)	\( r \)	9,55%	8,33%	7,08%
	\( \sigma \)	19,61%	19,96%	20,14%

К сожалению таблица не влезает на ваш экран. Попробуйте перевернуть телефон горизонтально или откройте страницу на десктопе.

Но еще более нестабильны коэффициенты корреляции между активами, которые могут колебаться в широких пределах и очень быстро. На рисунке показана оценка корреляции между индексом облигаций и индексом S&P 500. Ширина окна 36 месяцев.

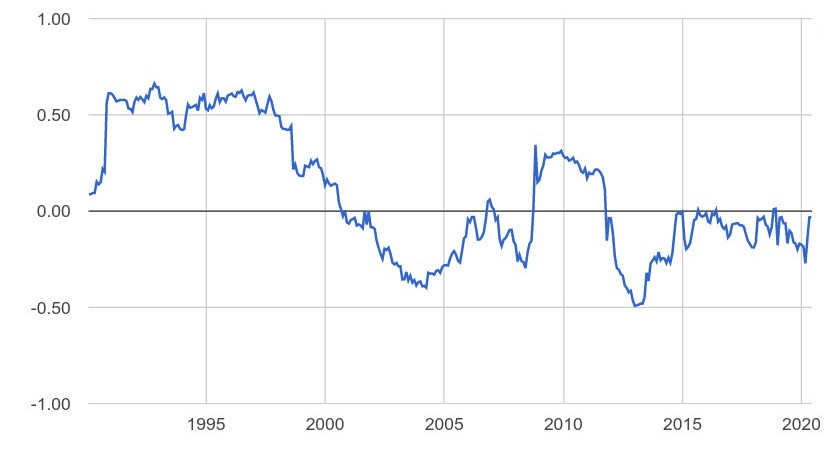
Величина колеблется в пределах от -0,492 до +0,663. Достаточно посмотреть на графики выше, чтобы увидеть, что форма границы эффективности при \( \rho=-0,5 \) и \( \rho=0,5 \) отличаются принципиально. При этом среднее за этот период значение 0,08 не говорит, по сути, ни о чём.

Выше уже упоминались другие проблемы:

• Метод предполагает фиксированный и известный горизонт инвестирования, однако, особенно на длительных интервалах времени, планы и обстоятельства инвестора могут существенно измениться.
• Само понятие вероятности имеет недостатки. Строго говоря про вероятности можно говорить только для бесконечно повторяемых событий. То есть надо вообразить параллельные миры или возможность бесконечно проживать один и тот же период.

Описанные выше построения не требуют принятия каких-либо гипотез по форме распределения вероятностей активов. Однако этот подход годится только до того момента, пока нам достаточно оценить среднюю ожидаемую доходность и СКО портфеля.

В рамках этой модели нельзя ответить на очевидный вопрос: какой максимальный убыток может быть в конце периода инвестирования?

Для того, чтобы сделать такую оценку, уже нужно принимать какие-то гипотезы по формам распределений. При этом результат будет сильно отличаться, в зависимости от принятых допущений.

Так, например, если принять, что доходности активов распределены нормально (или логнормально), то вероятность крупных убытков (и крупных прибылей) очень мала. Но есть существенные основания полагать, что в реальности хвосты распределений имеют не экспоненциальный, а степенной характер. То есть вероятность крупных движений многократно выше, чем предсказывается нормальным распределением.

Некоторые абсурдные следствия

Почему обычно рассматриваются только портфели с положительными весами? Потому, что если допустить возможность отрицательный весов, то получается вечный двигатель.

Посмотрим снова на наш пример с двумя активами:

• Актив 1: ожидаемая доходность \(r_1=6%\); СКО \( \sigma_2=4% \)
• Актив 2: ожидаемая доходность \(r_2=10%\); СКО \( \sigma_2=16% \)

Очевидная идея − осуществить короткую продажу актива 1 и на вырученные деньги приобрести актив 2. Тогда короткая позиция будет иметь ожидаемый убыток \(r_1=-6%\), но он будет с лихвой компенсироваться прибылью по длинной позиции \(r_2=10%\). А самое главное, доходность можно увеличивать бесконечно, не имея никаких вложений. То есть можно бесконечно продавать актив 1 и на вырученные деньги покупать актив 2, и получать в итоге бесконечно большую прибыль.

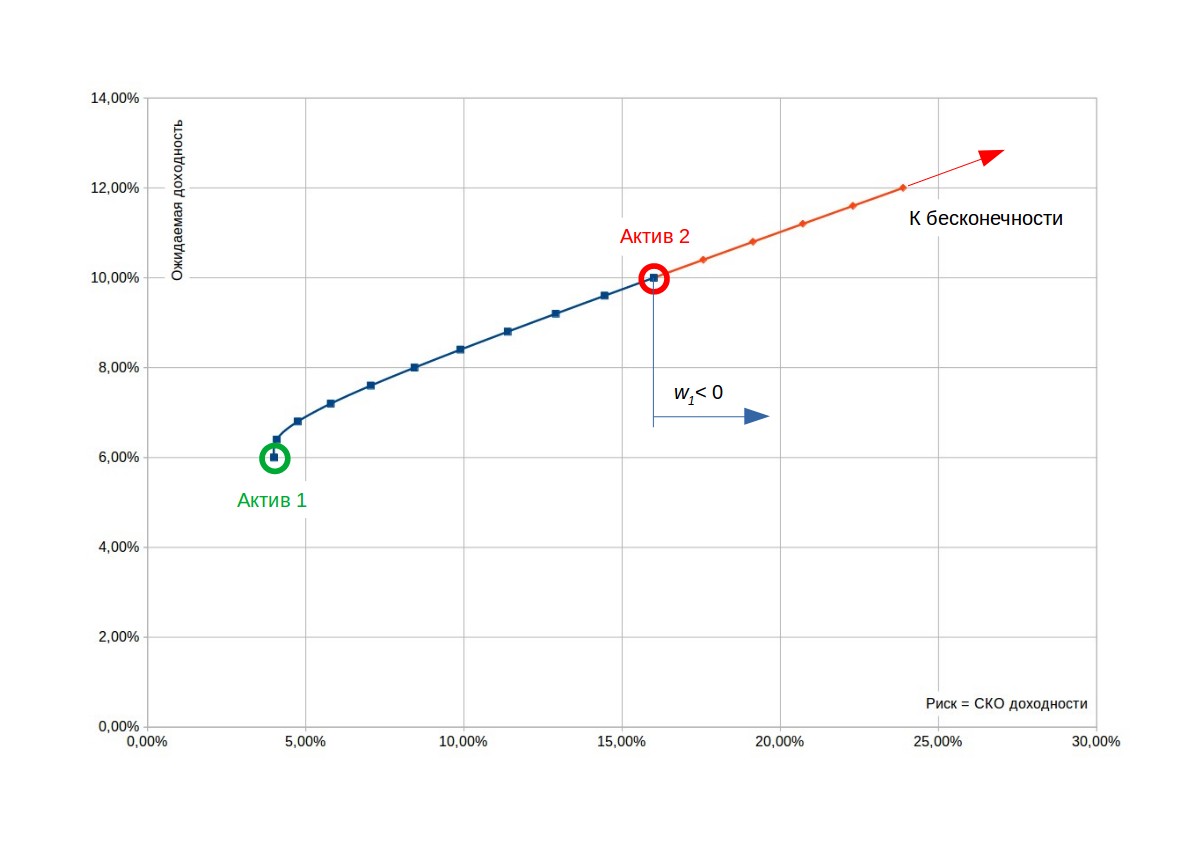
Почему это не работает в реальном мире? Потому что реальный мир не линеен. Для того, чтобы осуществлять короткую продажу актива 1, трейдер должен предоставить обеспечение в размере, равном его обязательствам. Этим обеспечением является его позиция в активе 2. Но если цены на рынке будут двигаться в неблагоприятном направлении: актив 2 будет падать в цене, а актив 1 расти, пусть даже временно, обеспечения станет недостаточно, и для трейдера наступит марджин кол (margin call). То есть брокер обратится к нему с требованием предоставить дополнительное обеспечение или начнет принудительно закрывать его позиции.

Это делает задачу нелинейной. Нам уже недостаточно знать только среднюю ожидаемую доходность, нам теперь надо еще понимать, насколько позиция может “просесть” за время жизни портфеля. Это, в свою очередь, влечет необходимость знать форму распределения вероятностей и много других параметров (таких, как автокорреляция). А это уже совсем другая модель.

В каком-то смысле проблема тут такая же, как и с системой мартингейл.

Напомню, что система мартингейл − это алгоритм выигрыша в азартные игры, например, в рулетку. Если упрощенно, выглядит он так: надо начать с небольшой ставки. Если выигрыш − забрать деньги и начать снова. Если проигрыш, удвоить ставку. Если удвоенная ставка выиграет, то выигрыш компенсирует потери по предыдущей ставке и принесет некоторую прибыль сверху. Если вторая ставка проиграла, надо снова удвоить ставку, и так до того момента, пока ставка не сработает, после чего начать заново.

В азартной игре система мартингейл не может проиграть, так как рано или поздно игроку улыбнется удача, и он компенсирует все свои вложения и получит прибыль. Таким образом система является беспроигрышной.

В чём же проблема? Проблема в том, что если игрок столкнется с серией проигрышей, то требуемый размер ставок очень быстро вырастает до астрономических размеров. Ни один реальный игрок с ограниченным запасом денег (в игровой индустрии его называют банкролл) не может этого выдержать. Есть вероятность, что он проиграет всё и не сможет продолжать игру, а это значит, что он потеряет всё.

Примерно то же и в ситуации с портфелем, содержащем короткие позиции. Теоретически имеется ожидаемая положительная доходность, но реальный инвестор с реальными и ограниченными финансовыми возможностями может не выдержать возникшего убытка. После чего будет вынужден сбросить позиции и вылетит с рынка (такова вкратце история краха фонда LTCM).

Рассмотрим еще одно возможное рассуждение. Ранее мы уже установили, что портфель с максимальным коэффициентом Шарпа − это наиболее эффективный портфель с точки зрения соотношения риска и доходности. Посмотрим на рисунок еще раз:

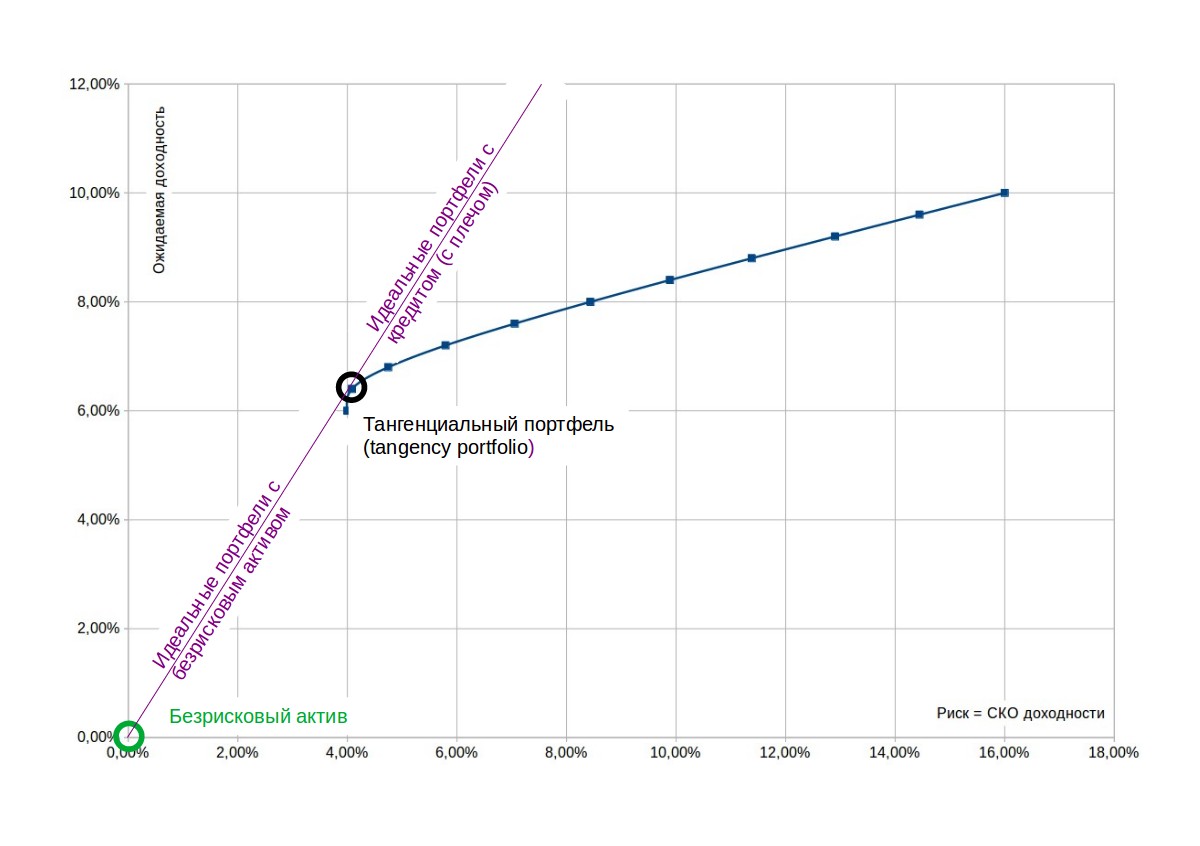
Рассмотрим портфель, состоящий из 2 активов: тангенциальный портфель и безрисковый актив. Поскольку актив является безрисковым, его коэффициент корреляции с портфелем равен нулю, так как его доходность гарантирована и не зависит ни от чего.

Как было показано выше, при нулевой корреляции граница эффективности представляет собой прямую линию, проходящую между активами. Это линия распределения капитала (capital allocation line).

Так как линия распределения капитала является касательной к границе эффективности, она будет в любой точке выше ее, то есть будет иметь более высокую доходность при том же риске.

Таким образом из теории получается, что инвестору надо всего 2 компонента:

• Безрисковый актив,
• Оптимальный по Шарпу портфель всех рисковых активов.

Все оптимальные портфели будут находится на линии распределения капитала. Если инвестор желает получить уровень риска ниже, чем у касательного портфеля, он комбинирует его с безрисковым активом. Если же инвестор хочет получить больший риск (и большую доходность), он осуществляет короткую продажу безрискового актива и вкладывает все полученные от нее средства в портфель, оптимальный по Шарпу.

Можно пойти еще дальше. Предположим, что все инвесторы на рынке используют приблизительно одни и те же данные и одни и те же методы. Тогда они все придут к одному и тому же выводу. То есть они все будут видеть один и тот же оптимальный портфель и инвестировать в него.

Это своеобразный “конец истории”, только его инвестиционная версия.

Где ошибка в рассуждениях? Ошибок множество:

• Возможность короткой продажи безрискового актива означает, что трейдер имеет возможность привлекать финансирование по безрисковой ставке. Это предположение очень далеко от практики. В реальности ни один трейдер не имеет такой возможности.
• Даже если предположить, что есть возможность привлечения финансирования по очень низким ставкам, то нужно иметь ввиду, что, как правило, маржинальное финансирование предоставляется с плавающей ставкой, которая пересчитывается каждый день. То есть, если мы говорим, что горизонт инвестирования 10 лет и всерьез рассматриваем вариант портфеля “с плечом”, то надо понимать, под какую ставку можно привлечь финансирование на 10 лет, а не на 1 день.
• Действуют все рассуждения, приведенные выше, про портфель с короткими позициями. Модель теряет адекватность, так как становится нелинейной. Возникает вероятность получить марджин кол.
• Ну и наконец, инвесторы имеют разное видение будущего и разные горизонты инвестирования, по этой причине рынок далек от того, чтобы прийти к консенсусу касательно “идеального портфеля” и инвестировать только в него.

Выводы

Несмотря на множество недостатков современная теория портфеля может быть полезным инструментом при планировании портфеля. Как и многие другие упрощенные модели.

Важно помнить, что полученный в результате MV-оптимизации портфель − это вовсе не истина в последней инстанции, а скорее некоторая пища к размышлению, черновик, над которым надо работать дальше.

Также всегда полезно “продолжить тренд” и посмотреть, что будет, если представить, что ничего не будет меняться. Такое мысленное упражнение уже может дать очень ценный взгляд вглубь вопроса. Например, отмести как нереалистичные некоторые сценарии.