Что такое метод дисконтированных денежных потоков?
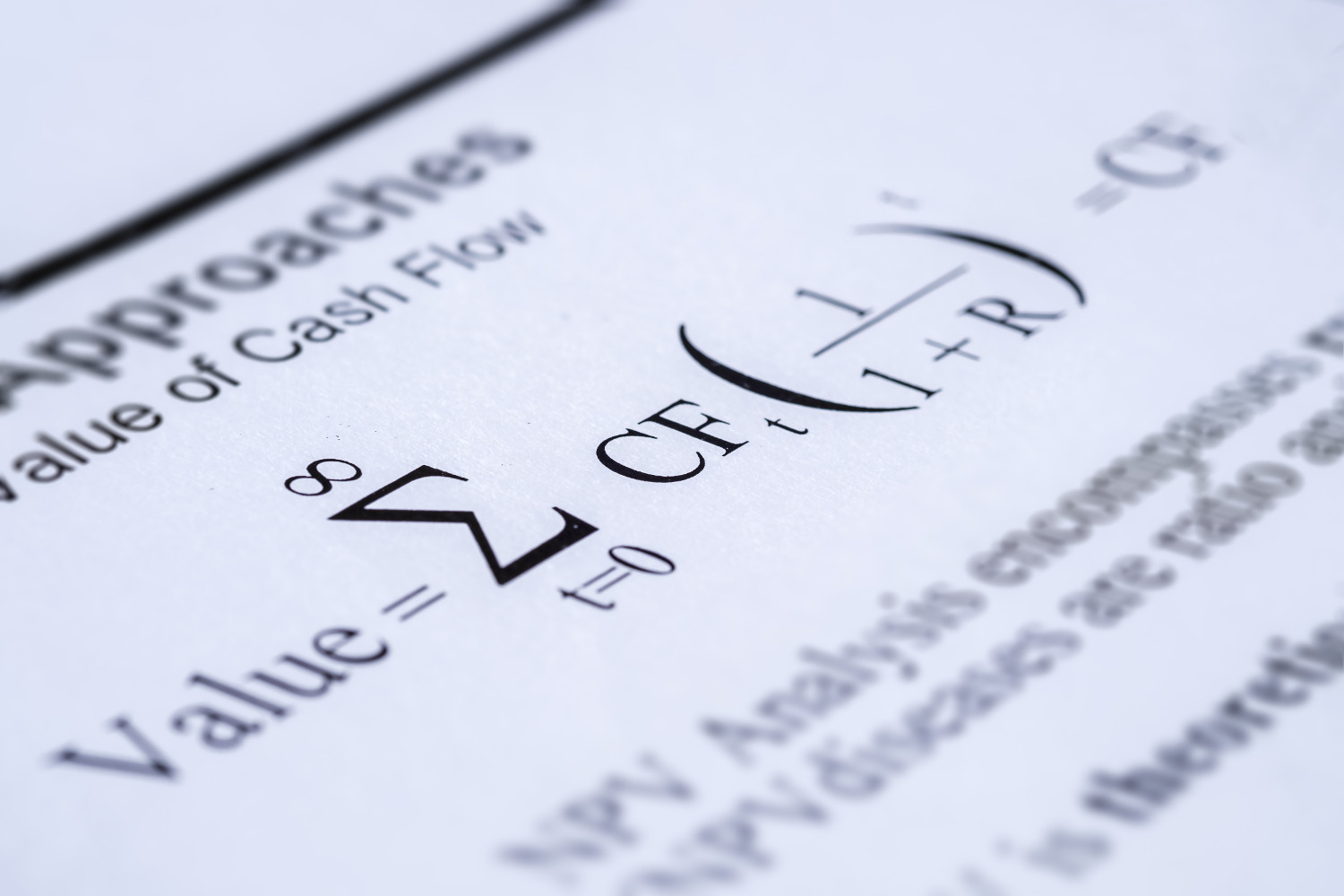
В этой статье я хочу рассказать о моделях дисконтированного денежного потока (DCF - Discounted Cash Flow), откуда они берутся и зачем они нужны.
Начнем с начала: данные модели нужны для оценки активов, таких как акции и облигации. Также этот подход может успешно применяться, например, для оценки доли в непубличном бизнесе, скажем, в ООО, да и, наверное, для оценки любой инвестиции. В основе метода лежит очень мощная идея о том, что справедливая цена актива определяется тем, сколько этот актив может принести денег в будущем.
DCF на примере облигации
Проще всего эту методику показать на примере облигации. Представим самую простую облигацию с постоянным купоном, к примеру 10%, выплачиваемым раз в год, сроком до погашения, скажем, 10 лет и номинальной стоимостью 100 рублей. Как определить справедливую цену за такую облигацию?
Посмотрим на то, сколько эта облигация принесет денег своему владельцу. Если не рассматривать возможность дефолта эмитента, то через десять лет инвестор получит номинал облигации (то есть 100 рублей) и 10 купонов по 10% от номинала, то есть еще 100 рублей. Итого в сумме 200 рублей.
Это первая важная цифра. Если воображаемый инвестор купил эту облигацию за 200 рублей, то через 10 лет он просто остается при своих, без прибыли и убытка. Таким образом, с точки зрения здравого смысла облигация не может стоит больше 200 рублей, поскольку если инвестор платит за неё больше, то это означает гарантированный убыток.
Тем не менее на момент написания статьи (весна 2020 года) облигации с отрицательной доходностью прочно вошли в обиход и уже никого не удивляют.
С точки зрения здравого смысла это абсурд, который пока что невозможно объяснить с позиций какой-либо экономической теории. Отрицательные ставки подрывают сам логический фундамент предмета, поскольку все рассуждения основаны на базовой аксиоме, что при прочих равных лучше иметь больше денег, чем меньше, и лучше раньше, чем позже. Даже если посмотреть на вопрос, как говорится, по-деревенски, то сажать, скажем, картошку имеет смысл только тогда, когда можно собрать больше, чем посадили. Иначе в чём смысл? В общем, этот феномен еще ждет своего объяснения, я же пока вернусь к старорежимной модели.
Итак, мы пришли к тому, что за время жизни облигации держатель получит в сумме 200 рублей. Много это или мало? Ответ на этот вопрос зависит от того, какие еще варианты вложения есть на рынке. Понятно, что если инвестор принял решение вложить деньги в облигацию из примера, то это значит, что он НЕ вложил их во что-то еще. Другие инвесторы рассматривают аналогичные инструменты и принимают свои решения. В итоге мы получаем фондовый рынок, на котором встречаются предлагающие капитал инвесторы и ищущие финансирование предприниматели. Часто, на самом деле, это одни и те же люди, просто выступающие то в одном качестве, то в другом.
Соответственно, на этом рынке устанавливается определенная процентная ставка, которая отражает баланс спроса и предложения на деньги. Если капитала на рынке много, а возможностей для его вложения мало, то ставки будут падать. Если же наоборот, интересных проектов много, а капитала мало, то ставки будут расти. Для полноты картины надо добавить еще ожидаемую инфляцию, но тут я не буду углубляться в этот вопрос.

Подчеркну, что нужно отличать реальную рыночную ставку от хотелок в голове у инвесторов и предпринимателей (которые естественным образом направлены противоположно). Так, например, инвесторы могут мечтать о какой угодно доходности, считать положение дел на рынке возмутительным, ссылаться на исторические данные, на принципы марксизма-ленинизма или теорию монетаризма, но факт тот, что рыночная ставка — это та ставка, под которую можно инвестировать деньги здесь и сейчас.
Инвестор, которого не устраивает текущая ставка, может попридержать деньги (и тем самым получить ставку ноль) и подождать момента получше, однако всегда есть шанс, что через год текущие ставки останутся в мечтах и сладких воспоминаниях, а им на смену придут еще более низкие.
Ну так вот, представим, что рынок решил, что нормальная ставка для вложения на 10 лет это, к примеру, 5% годовых. Это та ставка, которую можно получить здесь и сейчас, например, открыв депозит в надежном банке. Таким образом у нашего воображаемого инвестора есть 2 варианта:
- купить облигацию,
- положить деньги под 5% годовых на депозит.
Какова должна быть цена нашей облигации, чтобы эти два вложения были равноценны?
Поскольку облигация в примере купонная, то для того, чтобы получился полный аналог, надо открыть 10 депозитов. Девять из них будут реплицировать купоны, а один, самый большой, будет реплицировать сумму основного долга и последний купон (обычно они платятся вместе).
Первый купон будет выплачен через год и составит 10 рублей. Для того, чтобы получить такую же сумму, надо сейчас открыть депозит на год и положить на него 10/1,05=9,5238 рубля.
Второй купон будет выплачен через 2 года и составит снова 10 рублей. Чтобы воспроизвести этот купон надо открыть еще один депозит, в этот раз на 2 года и положить на него 10/1,05^2=10/1,1025=9,0703 рубля. Число в знаменателе это фактор дисконтирования, показывающий ожидаемую за два года “рыночную” доходность.
Аналогично можно сделать со всеми остальными выплатами. В последний год инвестор получает номинал облигации и последний купон. То есть 110 рублей. Для того, чтобы получить такую сумму через 10 лет, требуемая сумма депозита сегодня составит 110/1,05^10=110/1,6289=67,5305 рублей.
Денежный поток купонной облигации
| Год | Выплата в конце года | Фактор дисконтирования | Эквивалентный депозит |
|---|---|---|---|
| 1 | 10 | 1,0500 | 9,5238 |
| 2 | 10 | 1,1025 | 9,0703 |
| 3 | 10 | 1,1576 | 8,6384 |
| 4 | 10 | 1,2155 | 8,2270 |
| 5 | 10 | 1,2763 | 7,8353 |
| 6 | 10 | 1,3401 | 7,4622 |
| 7 | 10 | 1,4071 | 7,1068 |
| 8 | 10 | 1,4775 | 6,7684 |
| 9 | 10 | 1,5513 | 6,4461 |
| 10 | 110 | 1,6289 | 67,5305 |
|
|
|
Итого: | 138,6087 |
К сожалению таблица не влезает на ваш экран. Попробуйте перевернуть телефон горизонтально или откройте страницу на десктопе.
Таким образом мы пришли к тому, что для того, чтобы при рыночной ставке 5% собрать из депозитов аналог облигации, надо иметь 138 рублей 61 копейку (примерно). Собственно, это и есть справедливая стоимость облигации, определенная методом дисконтированного денежного потока.
Сумму, которую я обозначила как эквивалентный депозит, принято называть чистой приведенной стоимостью (Net Present Value — NPV).
Конечно, такой расчет является упрощенным. В реальности ставки дисконтирования на разные периоды могут быть разные, нужно учитывать периодичность выплаты купонов и кредитные риски. Однако общая идея остается такая же, как показано выше.
Обобщение DCF моделей на акции
Теперь сделаем следующий довольно революционный шаг. Представим, что акция это, по сути, то же самое, что облигация, но с 2 отличиями:
- нет срока погашения - бумага бессрочная;
- выплаты не гарантированы.
Первая особенность, на самом деле, не является проблемой. Представим ту же облигацию, что и в предыдущем примере, только без срока погашения. Предположим, она платит купонный доход в размере 10% от номинала каждый год и так вечно.
Если мы будем продолжать дисконтировать всё новые и новые купоны, то через какое-то время заметим, что вклад от каждой следующей выплаты становится всё меньше и меньше. Сумма при этом будет стремиться определенному значению. Можно показать, что сумма такого бесконечного ряда будет равна:
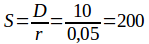
Где:
D - ежегодная выплата (в нашем примере 10 рублей),
r - ожидаемая рыночная доходность, которую мы используем для дисконтирования.
Таким образом, мы получили, что справедливая стоимость такой бесконечной облигации равна 200 рублей. Фактически это означает, что покупка данной облигации за 200 рублей принесет такой же доход, как бесконечная перекладка депозита под 5%. Формула, которую мы использовали, известна давно под названием формула суммы бесконечно убывающей геометрической прогрессии.
Правильное определение показателя r для акций — это весьма сложный, можно даже сказать, философский вопрос. Два аналитика с разным видением этого показателя получат разную оценку справедливой цены, даже если во всём остальном их мнения совпадают.
Тут я не буду глубоко погружаться в тему, замечу только, что при ставках, стремящихся к нулю, справедливые цены акций, определенные по модели дисконтированного денежного потока, стремятся к бесконечности. Смысл этого утверждения в том, что в мире, в котором нет роста (то есть ставки равны нулю), ценность любого актива, который может принести хоть какую-то прибыль, стремится к бесконечности.
С первой особенностью разобрались (хотя бы частично), перейдем ко второй. Аналогом купонной выплаты для акции является дивиденд, однако если компания не платит дивидендов, то это не значит, что она ничего не стоит, компания может инициировать дивиденд в будущем. То же верно наоборот, если компания платит дивиденд в данный момент, это еще не значит, что он останется неизменным навсегда. Он может расти или падать. Может вообще прекратиться.
В этом месте возможны 3 ответа, которые по идее должны приводить к одним и тем же выводам, но по-разному:
- Можно дисконтировать дивиденды. При этом если компания не платит дивиденды сейчас, то надо предположить, что она начнет их платить когда-то в будущем.
- Можно дисконтировать свободный денежный поток — показатель, который характеризует возможность компании платить дивиденды. Правда, само понятие свободного денежного потока можно определять несколькими разными способами.
- Можно дисконтировать чистую прибыль, которая тоже, в конечном счете, характеризует возможность компании что-то выплатить своим акционерам. Но проблема в том, что определение чистой прибыли сильно зависит от многих предположений, например, от срока амортизации основных средств, да и вообще подвержена манипуляциям.
Общая проблема всех этих методов, что нужно иметь видение касательно будущего эмитента. То есть надо сделать прогноз либо дивидендов, либо денежного потока, либо чистой прибыли, и всё это на бесконечно длинный горизонт времени. Оценка будет правильной, только если она опирается на правильный прогноз. Если прогноз ошибочный, то и оценка будет неверной.
Наиболее простой вариант — это предположить, что компания будет расти с постоянной скоростью. Такая логика приводит к модели роста Гордона, но это тема для отдельной статьи.
Несмотря на множество сложностей и недостатков я считаю, что всё же иметь несовершенную модель это лучше, чем не иметь никакой.





 soxic6
soxic6
