Черные лебеди, толстые хвосты и личный финансовый план

Составление личного финансового плана (как, впрочем, и любого другого плана) это всегда некоторая попытка предсказать будущее. В этой статье я постараюсь на простом примере показать, какие в этой связи возникают проблемы и как их можно преодолевать.

Итак, предположим, мы хотим решить следующую простую задачу: необходимо накопить 1 млн. рублей за 3 года, сколько нужно откладывать в месяц?

Идем по порядку, для инвестиций 3 года — это небольшой срок, поэтому вряд ли стоит думать о рисковых инструментах. На таком периоде лучше всего использовать облигации с минимальным кредитным риском, то есть облигации федерального займа (ОФЗ). В этом случае у нас не будет никаких ограничений на пополнение счета, докупить облигаций можно в любой торговый день (кратно 1 тысяче рублей).

Зайдем на сайт RusBonds и посмотрим какие-нибудь облигации с погашением через 3 года. В момент написания статьи на календаре 21 января 2020 года, поэтому задаем в поиске государственные облигации с погашением в 2023 году. Для того чтобы иметь гарантированный результат, выберем облигации с постоянным купоном.

Под наши условия идеально подходят облигации ОФЗ-26211-ПД с погашением 25 января 2023 года (то есть почти ровно через 3 года). На момент написания статьи такие облигации можно купить с доходностью в 5,605 %.

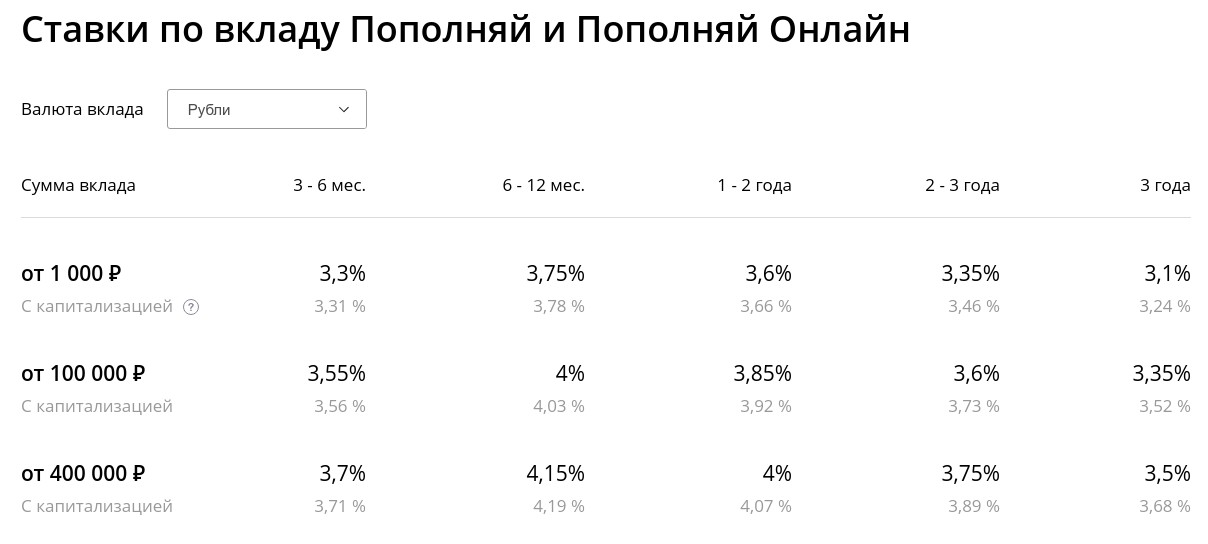
Кстати, для сравнения, в тот же момент вклад Пополняй в Сбербанке (с возможностью дополнительного внесения) можно открыть с доходностью максимум 4,15 %, это если оформлять вклад на срок от 6 до 11 месяцев и с начальной суммой 400 тыс. и более. Если же открывать вклад, как мы планировали, на 3 года и без начального взноса, то доходность упадет до 3,1%. Как обычно, в российских банках максимальные проценты при вкладе примерно на год, а на более длинные и более короткие вклады процент ниже.

При этом счет не позволяет никаких досрочных снятий, а облигации можно также и продать в любой рабочий день (без потери накопленного купонного дохода).

Не удивительно, что банков развелось, как грибов после дождя. Очень выгодный бизнес —привлекать депозиты под 3% и перекладывать их в гособлигации с минимальным риском дефолта под 5,5%. Хотя конечно, справедливости ради, замечу, что у других банков есть существенно более конкурентоспособные предложения.

Но вернемся к нашему финансовому плану. Собственно, теперь можно сделать табличку в Exсel и подбором установить, что для достижения цели нужно вносить 25 тыс. рублей в месяц. Примерно такая же методика заложена в простой калькулятор на моем сайте.

Казалось бы, вопрос решен, однако это не так, и дальше я поясню почему.

Добавляем неопределенность

Даже в нашем суперупрощенном примере мы, не совсем явно, сделали 2 весьма значительных допущения. Вот они:

• Доходность облигаций в будущем не изменится. То есть купоны по облигациям и новые взносы можно будет инвестировать по тем же ставкам, что и сейчас. Это предположение может оказаться неверным. Замечу, что всего полгода назад доходность выбранных нами облигаций составляла около 7%, а сейчас только 5,6%.
• Покупательная способность 1 млн. рублей через 3 года будет ровно такая, как мы ожидаем. То есть инфляции как бы нет, ну или мы изначально определили требуемую сумму с учетом роста цен и надеемся, что он будет ровно такой как ожидалось.

Замечу, что каждый из этих факторов может сработать как в минус, так и в плюс. Например, доходность облигаций может вырасти, а инфляция может оказаться наоборот, ниже ожиданий. Тогда финансовая цель будет достигнута раньше, чем предполагалось. Наоборот, если доходность облигаций упадет и/или инфляция превысит ожидания, то при том же взносе для достижения цели потребуется больше времени.

Та же проблема возникает, если вместо облигаций, скажем, открывать депозит на год и каждый раз после окончания срока добавлять деньги и открывать новый. Тогда мы можем быть уверены в ставке, которую мы получим на ближайший год, но не знаем наверняка, под какой процент мы сможем переложить депозит через год и тем более через два.

Проблема неопределенности становится еще серьезнее, если мы увеличиваем срок планирования и используем для инвестиций более рисковые активы, например, акции и облигации. Само понятие рискового актива говорит о том, что доходность не гарантирована и может колебаться в широких пределах.

Собственно, на самом деле даже безрисковая ставка не такая уж и безрисковая. Так, например, ставка ФРС США отражает то, под какой процент можно разместить средства сроком на 1 день. Соответственно, если ваш срок планирования больше одного дня, то эту ставку уже нельзя считать безрисковой, потому что завтра она уже может быть другая (как выше, так и ниже).

То есть когда говорят о безрисковой доходности, на самом деле, как правило, имеют в виду доходность без риска дефолта эмитента, оставляя риск реинвестиции купона за кадром.

То есть еще раз: даже при вложении денег в самые дубовые ультракороткие облигации (типа T-Bills) присутствует риск. Как правило, это риск получить доходность меньше, чем ожидалось за счет невозможности реинвестиции.

Что же можно сделать с неопределенностью? Можно просто не обращать на нее внимания, так как будто ее нет. Однако я считаю, что несовершенный план — это лучше, чем полное отсутствие плана, и предпочитаю использовать моделирование методом Монте Карло.

Моделирование методом Монте Карло.

Метод Монте Карло нашел широкое применение в финансовой практике. На моем сайте есть интерактивный калькулятор, построенный на простеньком алгоритме, использующем этот метод. Также для вероятностного моделирования есть множество коммерческих пакетов.

Основная идея заключается в том, чтобы считать подверженные неопределенности параметры случайными величинами. В нашем простом примере таких параметров два:

• доходность облигаций в зависимости от времени,
• инфляция за период 3 года.

Касательно первого пункта нам на самом деле нужно знать 41 параметр. Почему 41? Потому что мы будем пополнять счет 36 раз и нам нужно знать доходность, под которую мы будем инвестировать каждое пополнение. Первая доходность нам известна (это доходность на сегодня) остается еще 25. Плюс нам надо за это время реинвестировать 6 купонов (по 2 купона в год). Итого получается 41 неизвестная доходность.

В сумме у нас 42 параметра: 41 доходность и 1 накопленная за 3 года инфляция. Используем для определения недостающих данных генератор случайных чисел (тут есть кое-какая закавыка, но об этом подробнее в конце) и посмотрим, как будет расти наш счет. Взнос оставим неизменным.

Если нам повезло, и доходности оказались выше, чем мы ожидали, а инфляция при этом как ожидалось или ниже, то через 3 года сумма в реальном выражении будет больше, чем требуемый 1 млн. рублей. Если не повезет, то наоборот меньше.

Так мы получили одну реализацию случайного процесса. То есть один параллельный мир, в котором обстоятельства сложились определенным образом. Запишем результат и сгенерируем еще одну реализацию. Опять результат будет отличаться от теоретического в большую или меньшую сторону. Снова запишем результат и сгенерируем еще одну реализацию и так далее.

Через какое-то время мы наберем уже столько реализаций, что сможем оценить некоторые общие свойства.

Результаты будут тяготеть к среднему значению. Это то число, которое мы посчитали в самом начале. То есть при заданных выше характеристиках (взнос 25 тыс. в месяц, доходность 5,6% в год и срок 3 года) среднее значение результата через 3 года будет примерно 1 млн. рублей (номинальных).

Однако теперь мы имеем не только средний результат, мы получим еще и размах возможных отклонений. Отбросим теперь 10% самых лучших реализаций и 10% самых худших.

Мы только что получили диапазон, в котором мы окажется с вероятностью 80% (строго говоря 81%). Верхний хвост — это оптимистичная группа сценариев. Вероятность, что будет так хорошо, 10% и меньше. Нижний хвост — это наоборот, пессимистичная группа, вероятность того, что будет так плохо, тоже 10% и менее.

По центру — базовый сценарий (или как еще говорят, центральная тенденция). Вероятность того, что будет лучше или хуже, чем базовом сценарии равна 50х50. Его можно посчитать без вероятностей и моделирования по простой процедуре, как в начале статьи. Так, например, без вероятностей работает простой калькулятор у меня на сайте.

Однако анализ базового сценария не позволяет ответить на детский вопрос: зачем существуют консервативные портфели? Почему все на свете не вкладываются в агрессивные инструменты, ведь доходность то больше?

Вероятностное моделирование позволяет четко ответить на этот вопрос: да, ожидаемая средняя доходность у агрессивного портфеля больше, но и разброс возможных результатов тоже шире. Поэтому агрессивный инвестор гораздо менее уверен в том, какой результат он в итоге получит. Особенно на коротком интервале.

Ну какая же математическая модель без ограничений. Тут их предостаточно.

Самая большая проблема моделирования

Самая большая проблема: откуда брать ожидаемые характеристики? Для того, чтобы генерировать неизвестные параметры, нужно знать их статистические характеристики, но откуда их взять?

Это, кстати, относится ко всем статистическим моделям, включая модели современной теории портфеля (MPT, Modern Portfolio Theory) и MV оптимизации (MVO — Mean Variance Optimisation) на основе теории Марковица.

Можно, конечно, дать очевидный ответ — давайте возьмем и просто оценим их по историческим данным. Что греха таить, примерно так же поступаю и я. Однако надо иметь ввиду, что в этом предложении содержится два громадных подводных камня, потому что если мы так поступаем, то мы, понимая это или нет, предполагаем что:

• Будущее будет похоже на прошлое — даже более того, будет его полной копией.
• Все дни в прошлом тоже были похожи друг на друга — опять же не просто похожи, а полные копии.

Немного поясню свою мысль. Обычно мы берем, ну, к примеру, годовую доходность индекса S&P 500, скажем, за 20 лет и считаем среднее. Дальше мы используем это среднее для генерации случайных величин. Но это очень большое допущение. Когда мы так делаем, мы предполагаем, что доходность индекса, скажем, в 2009 году и в 2018 — это одна и та же случайная величина, с одним и тем же средним значением, одной и той же дисперсией и т.п.

Из этого допущения следует, например, что вероятность вырасти на 5% для рынка в 2019 году была ровно такая же, как и в 2009. Но ведь ситуация различалась кардинально! В 2009 году рынок лежал в руинах после падения на 51%, а по состоянию на 2018 год рынок непрерывно рос предыдущие 9 лет. Разве можно утверждать, что разницы нет!?

Еще более безумным выглядит усреднение за 100 и более лет. На самом деле историю доходностей индекса S&P500 за 100 лет правильнее рассматривать не как 100 реализаций одной и той же случайной величины, а как 100 случайных величин по одной реализации.

На эту тему можно много чего еще написать, но это выйдет далеко за рамки статьи.

Толстые хвосты, черные лебеди и всё такое

Как правило, для моделирования используются случайные числа, сгенерированные согласно нормальному распределению (оно же распределение Гаусса), но это очень спорно.

Опять же, по этому вопросу можно много чего написать. Например, один бывший опционный трейдер написал целую серию весьма увесистых трудов. Но если в двух словах: есть весьма веские основания полагать, что интересующие нас величины распределены вовсе не по нормальному закону.

Есть ряд наблюдений, которые позволяют утверждать, что действительное распределение имеет так называемые толстые хвосты. То есть вероятность очень больших отклонений от среднего гораздо больше, чем кажется.

Я в своих расчетах, как правило, предполагаю, что центральная часть распределения может быть примерно представлена нормальным распределением. Однако верхние 10% и нижние 10% это хвосты, которые вероятнее всего распределены по экспоненциальному закону.

Точное моделирование хвостовых рисков является пока что нерешенной задачей, однако модель, описывающая 80% ситуаций, на мой взгляд, уже хорошее подспорье. Повторюсь: на мой взгляд лучше иметь несовершенный план, чем вообще никакого.

Псевдослучайные числа

В заключении замечу, что я использую для калькулятора псевдослучайные числа, что безусловно негативно сказывается на качестве моделирования. Но в данном случае это обусловлено сугубо экономическими соображениями, поскольку слишком накладно встраивать в простой некоммерческий калькулятор подписку на внешний сервис физической генерации истинно случайных рядов. Ну или с бесплатной подпиской он бы работал нереально медленно. Так что прошу простить.